Sistemas Formales y su importancia

Un sistema formal es un tipo de sistema lógico-deductivo constituido por un lenguaje formal, una gramática formal que restringe cuales son las expresiones correctamente formadas de dicho lenguaje y las reglas de inferencia y un conjunto de axiomas que permite encontrar las proposiciones derivables de dichos axiomas. Los sistemas formales también han encontrado aplicación dentro de la informática, la teoría de la información, y la estadística, para proporcionar una definición rigurosa del concepto de demostración. La noción de sistema formal corresponde a una formalización rigurosa y completa del concepto de sistema axiomático, los cuales pueden ser expresados en lenguaje formal o en lenguaje natural formalizado.

Se llama formalización al acto de crear un sistema formal, con la que se pretende capturar y abstraer la esencia de determinadas características del mundo real, en un modelo conceptual expresado en un determinado lenguaje formal.

En la Teoría de la demostración, las demostraciones formales pueden expresarse en el lenguaje de los sistemas formales, consistentes en axiomas y reglas de inferencia. Los teoremas pueden ser obtenidos por medio de demostraciones formales. Este punto de vista de las matemáticas ha sido denominado formalista; aunque en muchas ocasiones este término conlleva una acepción peyorativa. En ese sentido David Hilbert creó la disciplina denominada metamatemática dedicada al estudio de los sistemas formales, entendiendo que el lenguaje utilizado para ello, denominado metalenguaje era distinto del lenguaje del sistema formal que se pretendía estudiar. El lenguaje formal que se estudia, en este caso se llama también, en ocasiones, lenguaje objeto.

Un sistema así es la reducción de un lenguaje formalizado a meros símbolos, lenguaje formalizado y simbolizado sin contenido material alguno; un lenguaje reducido a mera forma que se expresa mediante fórmulas que reflejan las relaciones sintácticas entre los símbolos y las reglas de formación y transformación que permiten construir las fórmulas del sistema y pasar de una fórmula a otra.

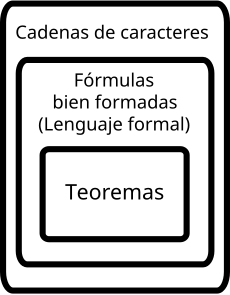
La utilidad e importancia de un sistema formal es señalar como válidas determinadas cadenas. Estas cadenas válidas se denominan teoremas. Para obtener los teoremas se emplean las reglas de producción que convierten una cadena en otra. Hay ciertos teoremas iniciales que no se obtienen de ninguna regla, éstos son los axiomas que se suponen válidos por definición y se convierten en el germen de producción de teoremas.

Con el desarrollo de los sistemas formales se abrió la expectativa de poder reducir la demostración a cálculo, y con ello se produjo una gran esperanza que llevó a la búsqueda de la pretendida demostración automática, es decir de procedimientos para la definición de algoritmos capaces de construir la secuencias de fórmulas que formen una demostración.